√ 3 / √ 4 which is √ 3 / 2 Solve Quadratic Equation using the Quadratic Formula 34 Solving x 2x1 = 0 by the Quadratic Formula According to the Quadratic Formula, x , the solution for Ax 2 BxC = 0 , where A, B and C are numbers, often called coefficients, is given byEvaluate (√2√3)^2(√5√2)^2Evaluate (Root 2 Root 3)2 (Root 5 Root 2)^2Here, a = 1 is the real cube root of unity while a = – ½ i √(3/ 2) and a = – ½ – i √(3/ 2) are the imaginary or complex cube roots of unity How to Find Cube Root of Unity Values (Derivation)?

Ml Aggarwal Solutions For Class 10 Chapter 5 Quadratic Equations In One Variable Free Pdf Available
3/20
3/20-The value of √52√6 is √3−√2 √3√2 √5√6 none of these Please scroll down to see the correct answer and solution guide2√3/2 का स्क्वायर रूट कैसे निकालें?




The Square Root Of 1 3 4 4 2 1 3 4 1 3 4 2 2 1 3 2
Sin30°Cos30°=(1√3)/2 Reason why I didn't add 1 and √3 together is that, according to the rules of surds, numbers don't add each other except they have the same irrational numbers eg √3 √3 = 2√3, you only add the numbers outside and for that there's an invisible 1 there B √3/2 C √2/2 D 1/2 Answers 1 Get ↓ Other questions on the subject Mathematics Mathematics, 10, sara66 Which of the following correctly justifies statement four of the two column proof?State, Whether the Following Numbers is Rational Or Not ( 3 √3 )2 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 5 Question Bank Solutions Concept Notes & Videos 261 Syllabus Advertisement Remove all ads State, Whether the Following Numbers is Rational Or Not ( 3 √3 )2
3 x 2 3 2 3 2 3 2 3 x 2 3 2 3 2 4 4 3 3 7 4 3 11 3 a b 2 a b 1 a b xa 2 b 2 a b from SOCI 4103 at Memorial University of Newfoundland This preview shows page 3 9Start studying Standard angles Learn vocabulary, terms, and more with flashcards, games, and other study tools$$\cos210°={√3}/2$$ #3 Know How to Solve for Tangent Lastly, it's essential to know how to use all of this information about the trig circle and sine and cosine in order to be able to solve for the tangent of an angle In trig, to find the tangent of an angle θ (in either degrees or radians), you simply divide the sine by the cosine
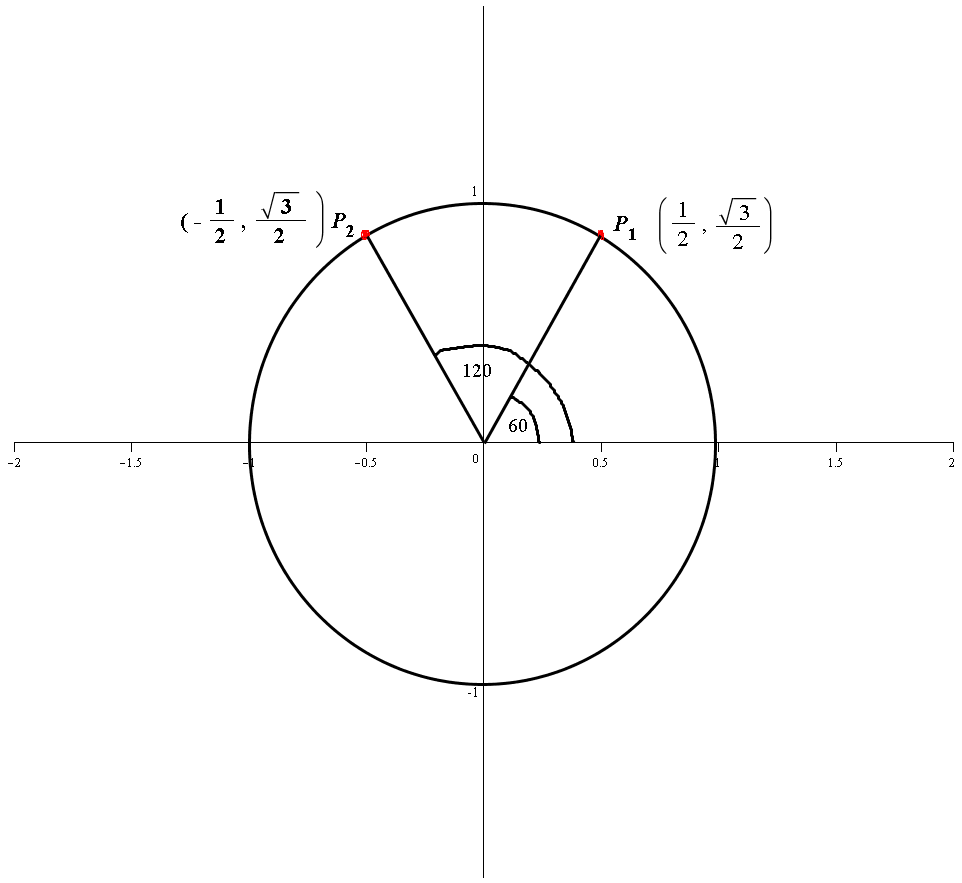
If the latus rectum of an ellipse is one half of its minor axis, then its eccentricity is A 1/2 B 1/√ 2 C √3/2 D √3/4 asked 1 day ago in Ellipse by Eeshta01 ( 238k points) ellipseTherefore we end up with (1/2, √3/2) and can conclude that sin(1°) or sin(2π/3) is equal to 1/2 and cos(1°) or cos(2π/3) is equal to √3/2 Finding Sine and Cosine Third Quadrant This is exactly the same as Finding Sine and Cosine Second Quadrant , except for step five, we now negate both value of the ordered pairIn this type of right triangle, the sides corresponding to the angles 30°60°90° follow a ratio of 1√ 32 Thus, in this type of triangle, if the length of one side and the side's corresponding angle is known, the length of the other sides can be determined using the above ratio



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community




Precalculus Review Calculus Preview Cool Math Com The Unit Circle Unit Circle Studying Math Math Geometry
And the height of a triangle will be h = √3/2 * a which is the exactly value of the apothem in this case We remind you that √ means square root Using this we can start with the maths A₀ = a * h / 2 = a * √3/2 * a / 2 = √3/4 * a² Where A₀ means the area of each of the equilateral triangles in which we have divided the hexagonDefinition Orthogonal Matrix For a square matrix 𝐴 to be orthogonal, it must be the case that 𝐴 𝐴 = 𝐼, where 𝐴 is the matrix transpose of 𝐴 and where 𝐼 is the 𝑛 × 𝑛 identity matrix If we were to take a random square matrix, then it is very unlikely that this matrix would also be orthogonal C is the circle with equation x^2 y^2 = 1 Q(1/2, √3/2) is the point on C The equation of the tangent to C at the point Q can be written in the form y = axb Find the value of a and find the value of b Categories Mathematics Leave a Reply Cancel reply Your email address will not be published Required fields are marked *




Find The Square Root 1 3 2 4 Ppt Video Online Download




Multiplying And Dividing Radical Expressions
The Sierpinski triangle (pictured below) is a fractal image The original figure is an equilateral triangle In each step, the computer splits every triangle in the design into 4 congruent equilateral triangles, and removes the center one from the design The area remaining in a particular design after n steps can be shown using the following expression 25√3 / 2 = 3(2√3 – 2√7 – 3 √21)(√7 – 2) = 3(2√21 – 14 – 3√7 7√3 – 4√3 4√7 6 – 2√21) = 3(3√3 √7 – 8) Question 3 If (x – a) is a factor of the polynomials x 2 px – q and x 2 rx – t, then prove that a = \(\frac{tq}{rp}\) Solution Let f(x) = x px q and g(x) = x 2 x – t Find parametric equations for the tangent line to the curve x=2 sin t, y= 2 sin 2t, z=2 sin 3t at the point (1, √3, 2) Graph the curve and the tangent line on a common screen



If The Point X Sqrt 3 2 Is On The Unit Circle What Is X Socratic




Find F X 3x 2 4 F X 2 Square Root X 3 2 Chegg Com
If the latus rectum of an ellipse is one half of its minor axis, then its eccentricity is A 1/2 B 1/√ 2 C √3/2 D √3/4 asked 5 days ago in Ellipse by Eeshta01 ( 244k points) ellipseClick here👆to get an answer to your question ️ Simplify the following expression ( 3 √(3)) ( 2 √(2))SOLUTION √8=2√2 so 1÷ (√√2)=1÷ (2√23√2) =1÷ (√2) so answer is 1÷√2 Like if satisfied




Square Root 3 2 Square Root




Rationalize 1 7 3 2 Maths Questions
See the answer See the answer See the answer done loading help with both please Show transcribed image textRationalise the Denominators of 2 √3 / 2 √3 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 5 Question Bank Solutions Concept Notes & Videos 261 Syllabus Advertisement Remove all ads Rationalise the Denominators of 2 √3 / 2 √3 MathematicsExample 1 In the above Table, left column, it is found that cos30° = √3/2Since sin30° = 1/2, we may use sin 2 (30°) cos 2 (30°) = 1 to solve for cos30° Solution Substituting for sin(30°), we get (1/2) 2 cos 2 (30°) =1, or, cos 2 (30°) = 3/4, or, cos(30°) =√3/2 Example 2 In the above Table, middle column, it is found that tan30° =√3/3




Graph Graph Equations And Equation Systems With Step By Step Math Problem Solver




Chapter 7 Radicals Radical Functions And Rational Exponents Ppt Video Online Download
If y(x) is solution of DE √(1x^2 ) dy/dx√(1y^2 )=0, Such that y(1/2)=√3/2 then(a) y(1/√2)=1/√2(b) y(1/√2)=√3/2(c) y(1/√2)=1/√2(d) y(1/2)=1/2To Transcript Example If A = 8(3&√3&2@4&2&0) and B = 8(2&−1&2@1&2&4) Verify that (i) (A')' = A, A = 8(3&√3&2@4&2&0) A' = 8(3&√3&2@4&2&0Sine calculator online sin(x) calculator This website uses cookies to improve your experience, analyze traffic and display ads




A1 2 B 3 2 H Square Root Of 2 2 Di Square Ro Gauthmath




Square Root 3 2 Square Root
Determine angle type 150 is an obtuse angle since it is greater than 90° tan (150) = √ 3 /3 In Microsoft Excel or Google Sheets, you write this function as√ 3 2 i We can subtract 1 from this to get −1 2 √ 3 2 i, and hence L(0,−1 2 √ 3 2 i), which is the same thing as the line 0 ∈ L(0,1)2π/3 If there were a general trisecting construction, we could use it to draw 0 ∈ L(0,1)2π/9 and then by intersecting with C(0;1), we would have constructed α= (1;√ 3 / √ 4 which is √ 3 / 2 Solve Quadratic Equation using the Quadratic Formula 46 Solving y 2y1 = 0 by the Quadratic Formula According to the Quadratic Formula, y , the solution for Ay 2 ByC = 0 , where A, B and C are numbers, often called coefficients, is given by




Square Root 2 3 Cannot Be Equal 1 3 1 2 2 6 2 2 3 2 3 1 4 3 1 2 Maths Number Systems Meritnation Com



Q Tbn And9gcqt8xcypqw0rmdh64vbuopwz1cxhnbqpt756epqa I9o2cblok Usqp Cau
As math(2\sqrt{3}) \cdot (2\sqrt{3})=1/math We have math\log_{(2\sqrt{3})}(2\sqrt{3}) \cdot (2\sqrt{3})=\log_{(2\sqrt{3})}1=0/math math\impliesAnswer The numbers √2 and √3 in the expression √2x√3 are surds because the roots of 2 and 3 can not be exactly determined They are irrational numbers Further, √2 and √3 are quadratic surds since the two surds are of the second order (The order of a surd is determined by the root symbolIf x = 2 √3 then the value of x 3 – x 3 is Given x = 2 √3 If x = 2 √3 then the value of x 3 – x 3 is A 30√3 B 30√3 C 30√2 D 30√2 Please scroll down to



2 Square Root 6 Times Square Root 3




Find Square Root Of 3 2 10i Brainly In
The remaining phasetoneutral voltage will be √ 3 /2 the phasetophase voltage So if AB, BC and CA are all 240 volts, then AN and CN will both be 1 volts, but BN will be 8 volts Other types of threephase supplies are wye connections, ungrounded delta connections, or cornergrounded delta ("ghost" leg configuration) connections Mathematics, 0100, bullockarwen Aplumber charges $50 to visit a house plus$40 for every hour of work define a variable and write an expression to represent the total cost of hiring a plumber Answers 3 continue Other tasks inA corresponding angles theorem b transitive property of equality c vertical angle theorem d substitution property of equality




Solved Find All Zeros Of The Polynomial Fx 2x4 2x3 7x2 3x 6 If Self Study 365




In A Triangle Abc If A 30 And B C 2 Sqrt3 Sqrt2 1 2 Sqrt
Calculate sec(210)° Determine quadrant Since our angle is greater than 180 and less than or equal to 270 degrees, it is located in Quadrant III Let's see how we can learn it 1In sin, we have sin cos In cos, we have cos cos, sin sin In tan, we have sum above, and product below 2For sin (x y), we have sign on right For sin (x – y), we have – sign on right right For cos, it becomes opposite For cos (x y), we√3/2 cos315 √2/2 cos(7π/4) √2/2 sin315√2/2 sin(7π/4)√2/2 cos330 √3/2 cos(11π/6) √3/2 sin3301/2 sin(11π/6)1/2 sin(π/4) √2/2 RECOMMENDED TEXTBOOKS Geometry for Enjoyment and Challenge New Edition Milauskas, Rhoad, Whipple 256 expertverified explanations Geometry Common Core




What Is X 3 2 In Square Root Form Novocom Top




Strategy And Trick To Find Square Root Of 8 2 15 Radical Expressions Youtube
Click here👆to get an answer to your question ️ Find the principal solution of the following equations sin x = √(3)2 So if you recall, the short leg is 1/2 the hypotenuse, so the ycoordinate is 1/2, and the long leg is √3 times the shorter leg, or (√3)/2, so the xcoordinate is (√3)/2 The coordinates of that point are ((√3)/2,1/2) Now use the identities in the previous step to find thatSuppose the cube root of 1 is "a", i e 3 √1 = a According to the general cube roots definition, a 3 = 1



Solve Equations With Square Roots Elementary Algebra




Solving Quadratic Equations By Square Root Method By
T10=√3/2 T11=1/2 And the matrix is T=1/2 √3/2;√3/2 1/2 If you have any questions regarding this answer let me know in comments section belowQuestion QUESTION 2 Find the exact value of sin(1959) √2√3 2 √2√2 2 √2√3 2 √2√3 4 QUESTION 3 Find the exact value sin(sin 91 8 31 8 wool IT O 8 This problem has been solved!Simplifying this we get 2√3 (3 5 2√5) = 2√3 (2–2√5) = 4√3 4√15 Now both √3 and √15 are irrational We know that rational * irrational is irrational so 4√3 and 4√15 are irrational And also irrational irrational is irrational Therefore 4√3 4√15 is irrational 8 views



Solved X 3 Square Root 1 3 Square Root 2 What Is X X Is A Binomial With A Mixed Radical And Constant Course Hero



Square Root Of The Proca Equation Spin 3 2 Field Equation S I Kruglov Free Download Borrow And Streaming Internet Archive
2π 9) = cos(2π 9)sin




Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 V



Arrange In Ascending Order Cube Root Of 2 Square Root Of 4 Forth Root Of 3 Sarthaks Econnect Largest Online Education Community




Example Find Solution Of Sin X Root 3 2 Class 11




Solution List All The Points On The Graph Of Y Tanx O The Interval Pi 5 Pi 2 That Have A Y Coordinate Of 1 Square Root Of 3




Extract The Square Root Of A 2 Left Frac Left 3a Sqrt A Right 2 Right Left Frac Left 3 Sqrt A Right 2 Right Frac 41a 16 1 Mathematics Stack Exchange




Graph Graph Equations And Equation Systems With Step By Step Math Problem Solver




Solved If X 3 2 2 Check Whether X 1x Is Rational Or Irrational Self Study 365



1



How Do You Find The Limit Of X 1 Sqrt X 3 2 As X Approaches 1 Socratic



If X 3 2 2 Then What Is The Value Of X 1 X Quora




After Rationalizing The Denominator Of 2 3 5 2 2 3 3 And Simplifying We Get A 3 15 B 10 4 6 19 Then The Value Of A B Is




Solve Sin X Sqrt 3 2 All Solutions Radians Youtube



Square Root Of 3 Wikipedia




Rational Exponents




2 3 2 2 9 Square Root Of 36 81 4 3 2 3 Gauthmath
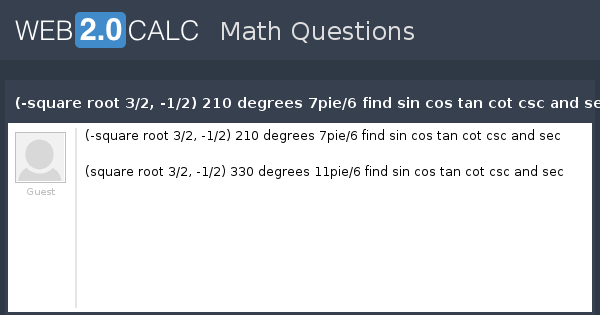



View Question Square Root 3 2 1 2 210 Degrees 7pie 6 Find Sin Cos Tan Cot Csc And Sec




Simplify 3 3 2 27 7 3 Brainly In




Solving Quadratic Equations
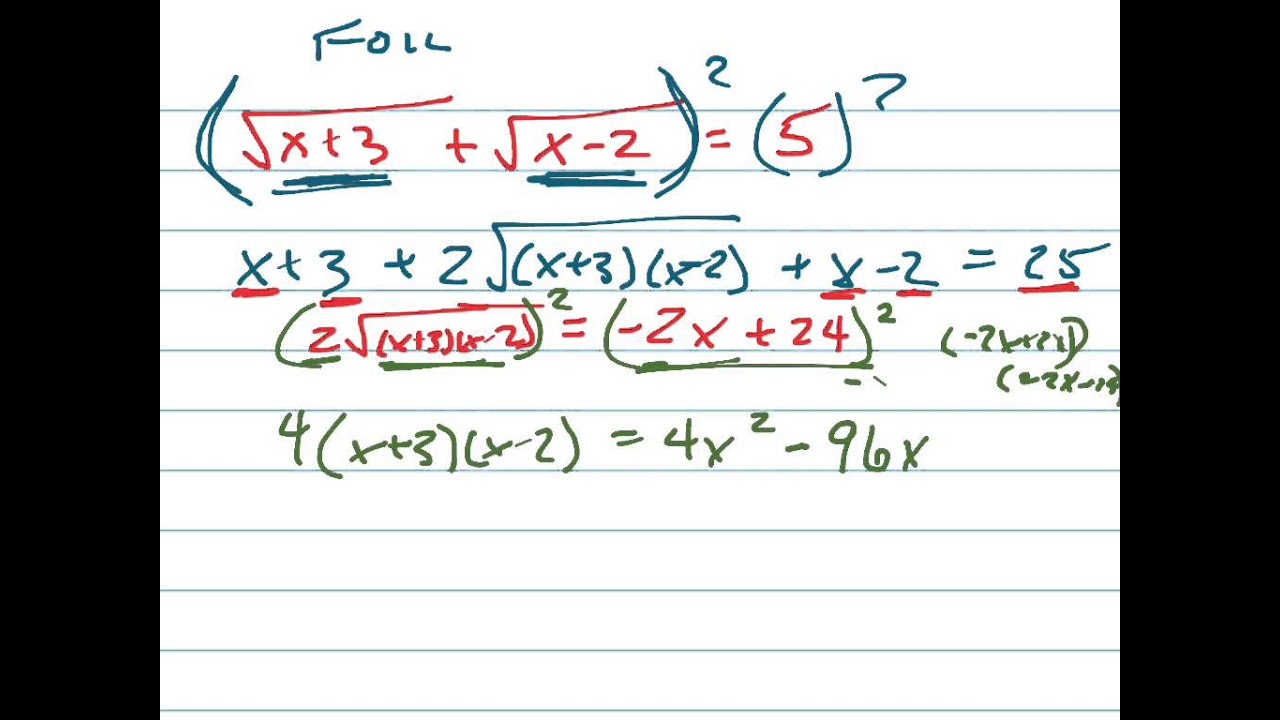



Solve Sqrt X 3 Sqrt X 2 5 Youtube




3 2 Square Root 3 By 3 Minus 2 Square Root 3 Is Equal To A B Square Root 3 Find Value Of A B All 3 Brainly In
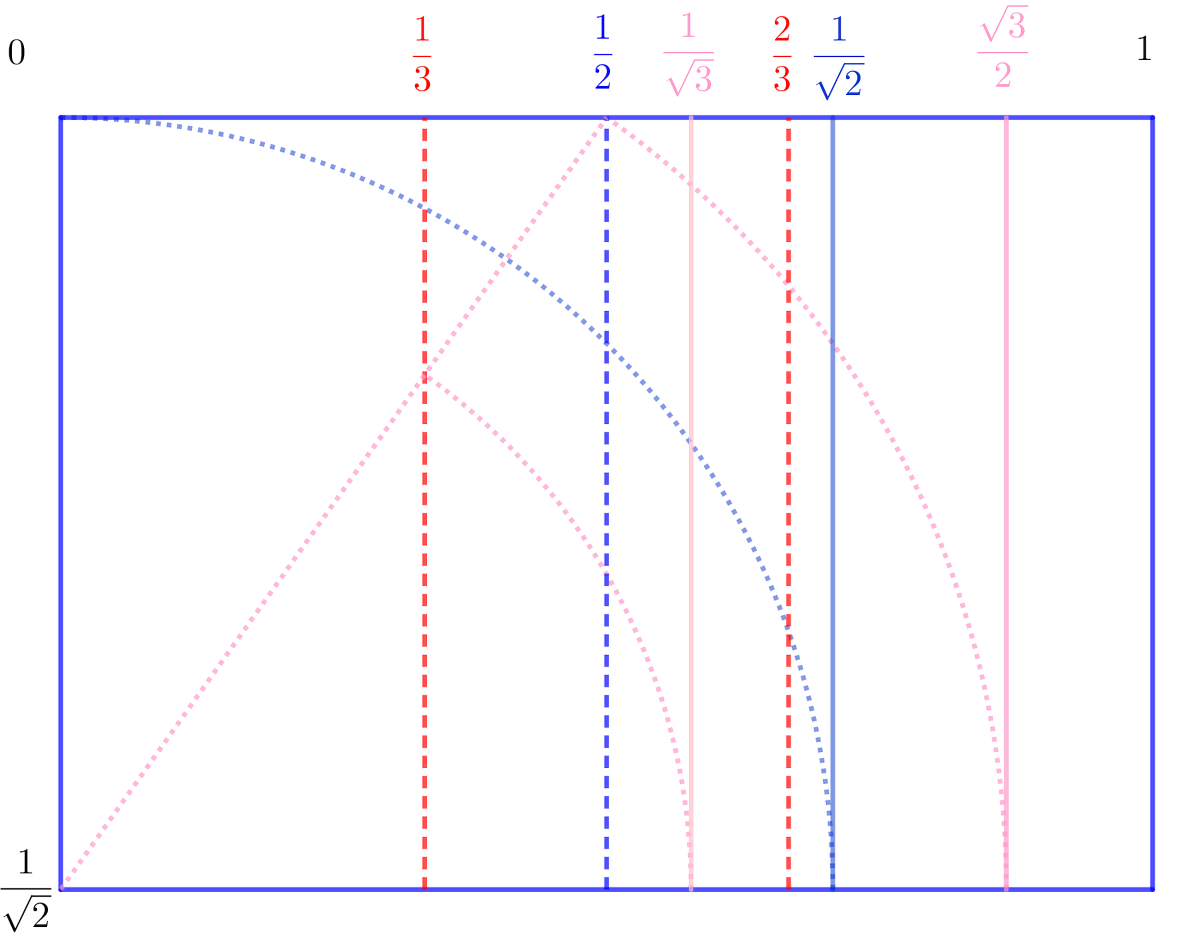



Christian Mercat And What Is A The Root Of Thirdsday Well The Inverse Of The Square Root Of 3 Day Which Is Easily Drawn On An Paper Reminding




The Square Root Of 1 3 4 4 2 1 3 4 1 3 4 2 2 1 3 2
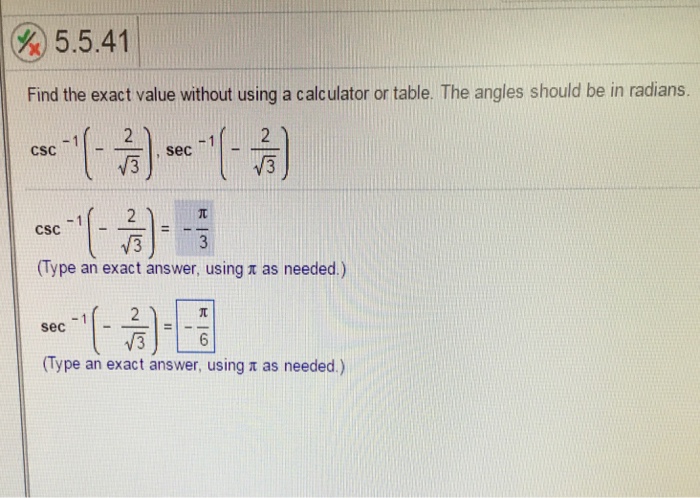



What Is The Answer To Sec 1 2 Square Chegg Com




What Is 3 2




Ml Aggarwal Solutions For Class 10 Chapter 5 Quadratic Equations In One Variable Free Pdf Available




1 2 3
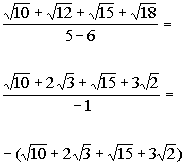



Rationalizing Denominators And Numerators Of Radical Expressions



Q Tbn And9gcqt8xcypqw0rmdh64vbuopwz1cxhnbqpt756epqa I9o2cblok Usqp Cau



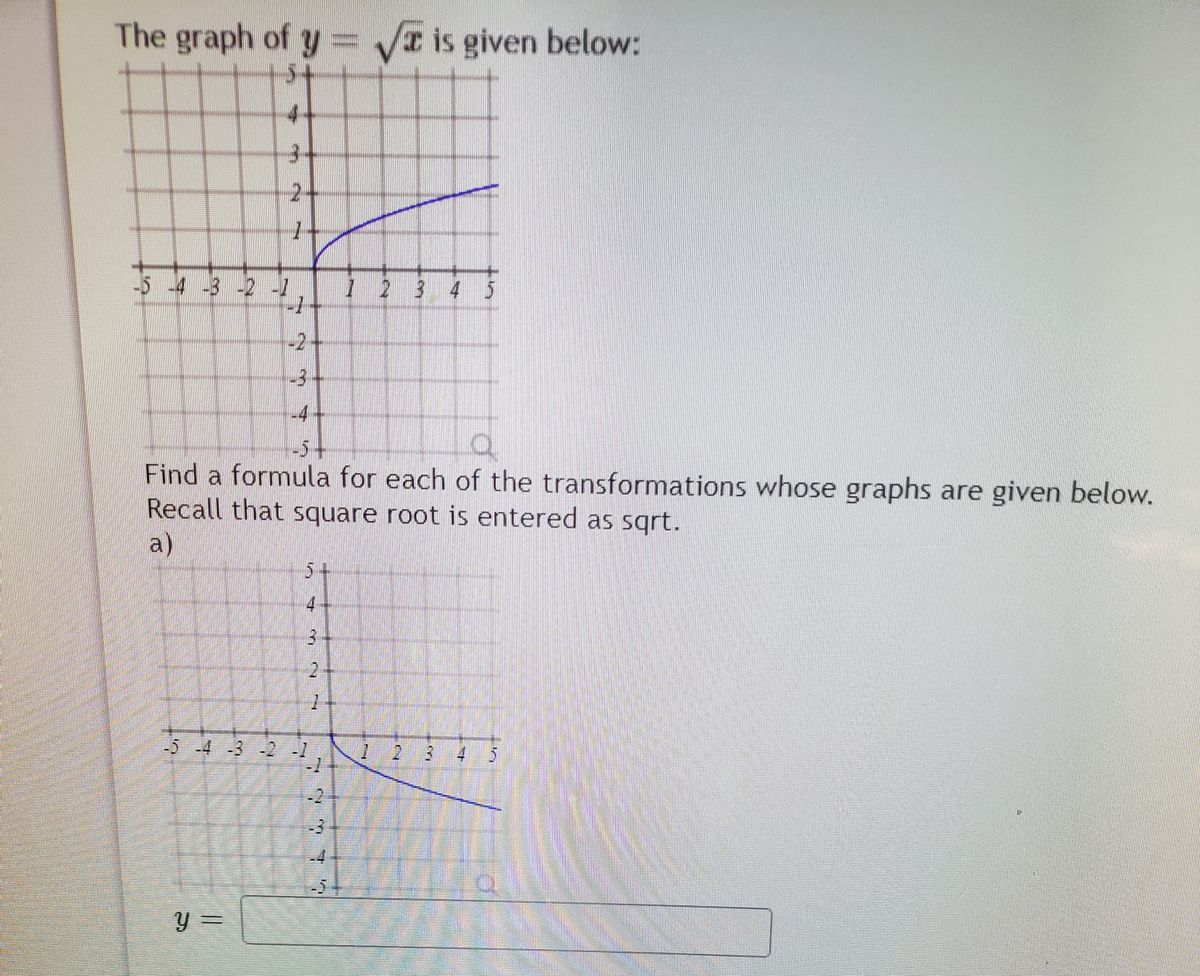
Answered The Graph Of Y Vt Is Given Below 4 Bartleby




What Is The Solution Of 2 3 2 3 Quora




Square Root Of 3 Wikipedia




Square Root Of 432 How To Find Square Root Of 432 Solved




Square Root Of 3 How To Find The Square Root Of 3




Using The Pythagorean Theorem Lesson 3 3 2



Www Sccollege Edu Departments Math Documents Math 185 11 05 006 Alternating Series Pdf




Multiplying And Dividing Radical Expressions



Transforming The Square Root Function Video Khan Academy



How To Simplify 3 2 2 With A Detailed Explanation Quora



Rationalizing The Denominator Chilimath



Answered 5 4 3 2 1 4 2 3 4 5 Find A Bartleby




Simplify 2 5 3 1 3 2 3 5 2



Www Pearson Com Content Dam One Dot Com One Dot Com Uk Documents Subjects Mathematics Worksheets Chapter2 Example 6 Chapter 2 Solving Quadratics By Completing The Square Pdf




30 60 90 Triangle Explanation Examples




Sin 1 Square Root 3 2 1 31 Cos 1 4 1 002 Chegg Com




Plot Of Peak Current Density Ip Versus Square Root Sweep Rate Y1 2 Download Scientific Diagram



Babylon And The Square Root Of 2 Azimuth




How To Multiply Square Roots 8 Steps With Pictures Wikihow




General Solution Of Sin4x Sqrt 3 2 Is Youtube
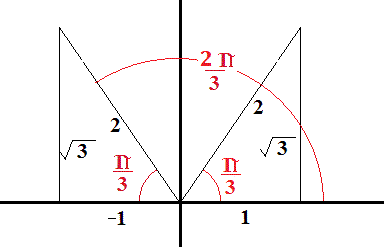



What Is The Sin 1 Sqrt 3 2 Socratic




Rationalize The Denominator Of 3 Minus Root 2 By 3 Root 2



What Is The Value Of 3 2 2 Quora




Example 18 Rationalize The Denominator Of 1 2 Root 3




How Do You Evaluate Cos 1 Sqrt3 2 Socratic




Ppt Surds Powerpoint Presentation Free Download Id




If X 3 2 3 2 Y 3 2 3 2 Find The Value Of X 2 Y 2 Xy Mathematics Topperlearning Com 9dqpqijj




Value Of Root 3 By 2
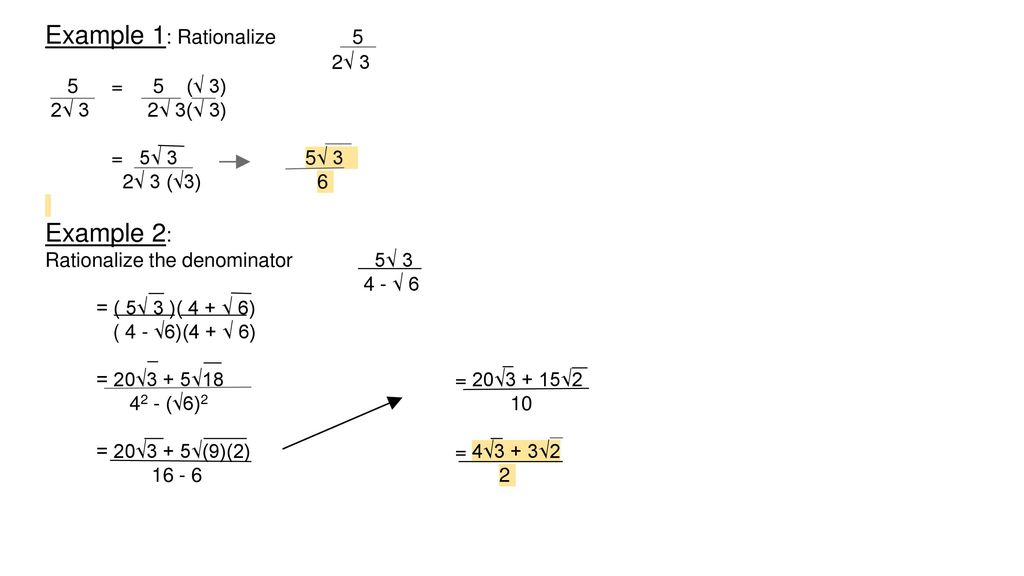



Chapter 5 Radical Expressions And Equations Ppt Download




Raney Distributions W 3 2 R X With Values Of The Parameter R Labeling Download Scientific Diagram



Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 Studyrankersonline




Simplifying Square Root Expressions Video Khan Academy




Rationalize The Denominator Of 1 3 2 Under Root 2 Under Root 5 Mathematics Topperlearning Com 8pvu0x66




Sin Theta Square Root 3 2 Novocom Top




How To Add And Subtract Square Roots 9 Steps With Pictures




Rationalise The Denominator Of 1 Root3 Root2 Brainly In
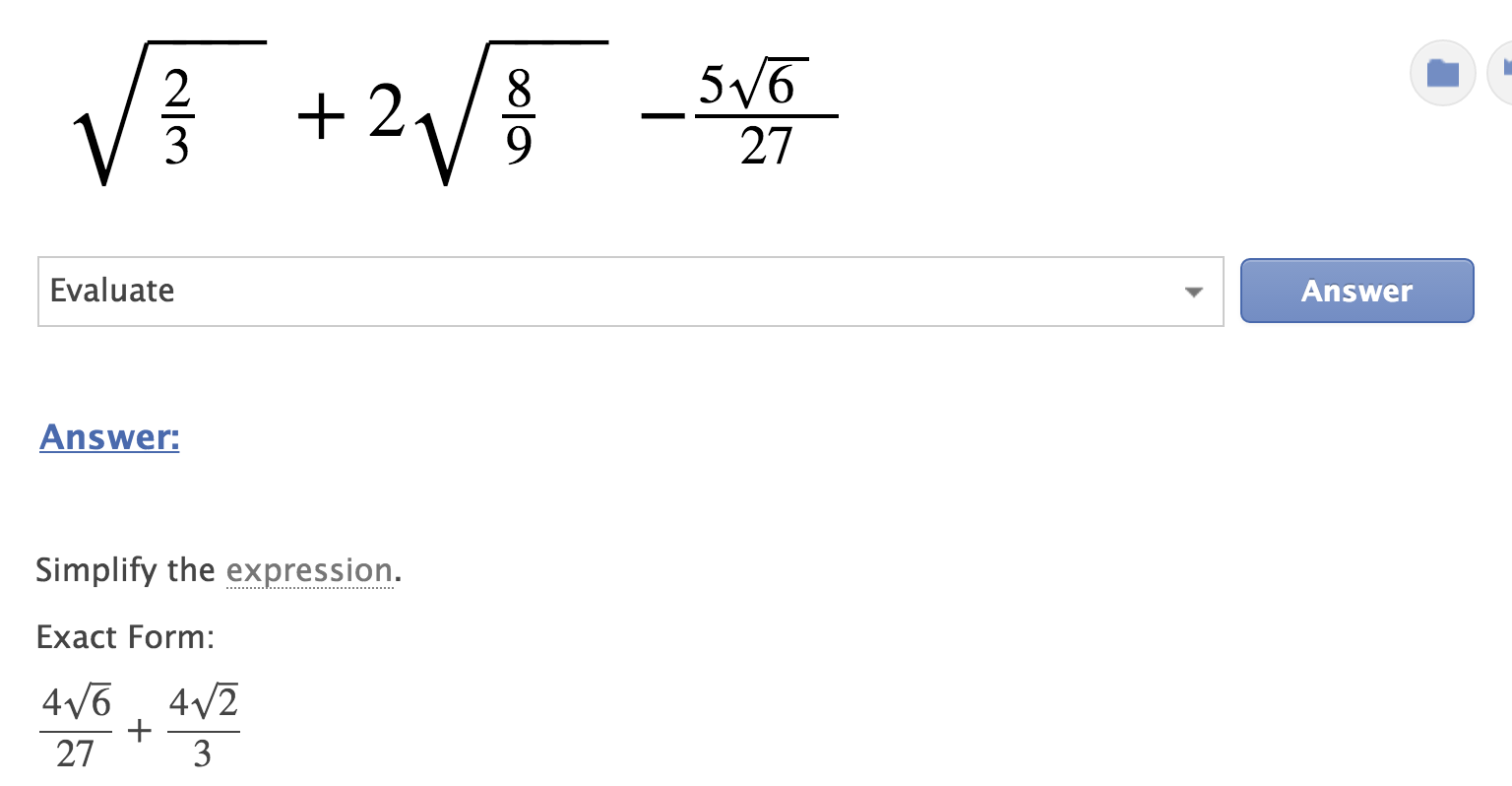



Squareroot 2 3 2 Squareroot 8 9 5 Squareroot 6 27 Chegg Com




Transforming The Square Root Function Video Khan Academy



Evaluate Under Root 3 Square 6 Cube 24 Studyrankersonline




A Cambridge Interview Problem Sqrt 3 2sqrt 2 Youtube




How To Multiply Square Roots 8 Steps With Pictures Wikihow



What Is The Positive Square Root Of 7 4 3 Quora




Square Root Of 2 Wikipedia
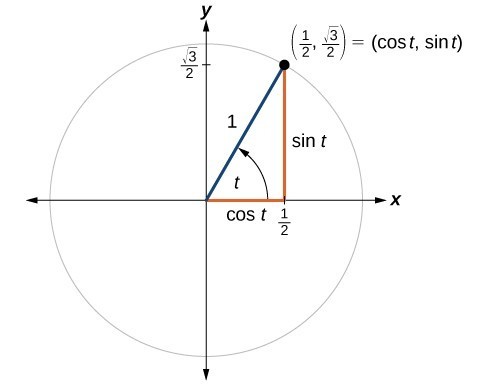



Unit Circle Sine And Cosine Functions Precalculus Ii




If N Square Root 3 2 2 Square Root 3 2 2 Square Root 3 1 2 Square Root 3 1 Then N Equal To 1 Maths Number Systems Meritnation Com




Simplify 3 5 5 2 4 5 3 2 With Video Teachoo Rationalising




Multiplying And Dividing Radical Expressions



Q Tbn And9gcqnfu4xl8biccm2lo1vb Feimstd8kb0bjmfkodcsezzh7idds Usqp Cau
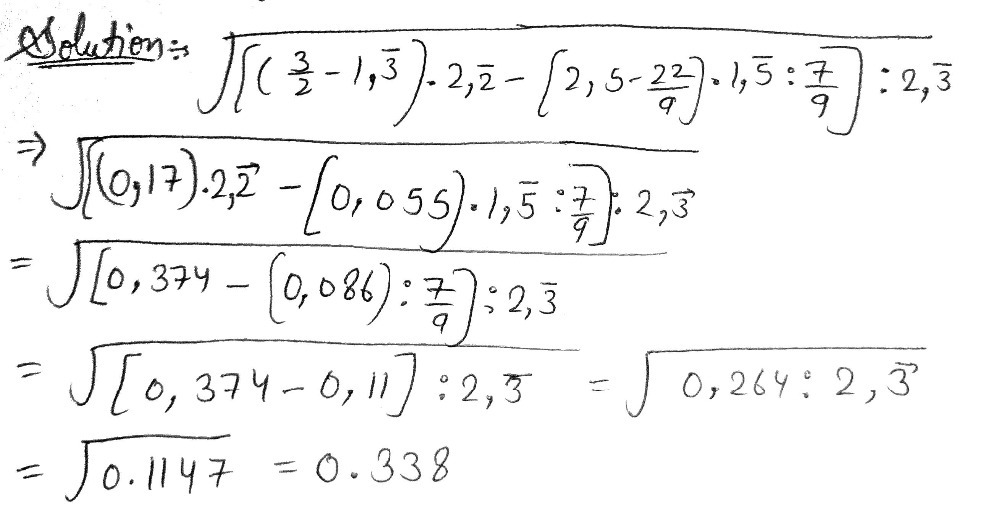



Square Root Of 3 2 1 Overline 3 2 Vector Gauthmath




Example 4 Graph A Translated Square Root Function Graph Y 2 X 3 2 Then State The Domain And Range Solution Step Graphing Quadratics Function Of Roots




4 The Square Root Of 3 Sqrt 5 Is A Sqrt 3 2 1 Sq



Solved Multiply And Simplify 3 2 Square Root 5 3 2 Square Root 5 Sorry No Square Root Button Course Hero



0 件のコメント:
コメントを投稿